2401. Breadth First Search

Given an undirected graph. Find the shortest distance between two specified vertices.

Input. The first line contains three positive integers n, s and f (1 ≤ s, f ≤ n ≤ 100). Here, n is the number of vertices in the graph, s and f are the initial and final vertices. The next n lines provide the adjacency matrix of the graph. If the value at the j-th element of the i-th row is 1, there is an edge between vertex i and vertex j.

Output. Print the minimum distance from the initial vertex to the final vertex. If no path exists, print 0.

Sample input	Sample output
4 4 3 0 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0	2

SOLUTION

graphs - bfs

Algorithm analysis

Find the shortest path in the graph from vertex s to vertex f using breadth first search.

Example

The graph given in the example, has the following form:

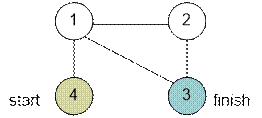
Algorithm realization

Declare an adjacency matrix g to store the graph and an array dist to store the shortest distances from the source to the vertices.

#define MAX 101

int g[MAX][MAX], dist[MAX];

The bfs function implements a breadth-first search starting from the vertex start.

void bfs(int start)

{

Initialize the dist array. If dist[i] = -1, it means that vertex i is not visited.

memset(dist, -1, sizeof(dist));

dist[start] = 0;

Declare and initialize a queue q.

queue<int> q;

q.push(start);

Continue the breadth-first search as long as the queue is not empty.

while (!q.empty())

{

Extract and remove vertex v from the front of the queue.

int v = q.front(); q.pop();

Where can we go from vertex v? Iterate over the edges v → to.

for (int to = 1; to <= n; to++)

If there is an edge from v to to and vertex to is not visited, then move to it (the edge (v, to) becomes an edge of the breadth-first search tree).

if (g[v][to] && dist[to] == -1)

{

Add vertex to to the end of the queue and compute the shortest distance dist[to].

q.push(to);

dist[to] = dist[v] + 1;

}

}

}

The main part of the program. Read the input data.

scanf("%d %d %d", &n, &s, &f);

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

scanf("%d", &g[i][j]);

Start the breadth-first search from vertex s.

bfs(s);

Print the shortest distance. If there is no path to vertex f (dist[f] < 0), set dist[f] = 0.

if (dist[f] < 0) dist[f] = 0;

printf("%d\n", dist[f]);

Algorithm realization – adjacency list

Declare an adjacency list g to store the graph and an array dist to store the shortest distances from the source to the vertices.

vector<vector<int> > g;

vector<int> dist;

The bfs function implements a breadth-first search starting from the vertex start.

void bfs(int start)

{

Initialize the dist array. If dist[i] = -1, it means that vertex i is not visited.

dist = vector<int>(n + 1, -1);

dist[start] = 0;

Declare and initialize a queue q.

queue<int> q;

q.push(start);

Continue the breadth-first search as long as the queue is not empty.

while (!q.empty())

{

Extract and remove vertex v from the front of the queue.

int v = q.front(); q.pop();

Where can we go from vertex v? Iterate over the edges v → to.

for (int to : g[v])

If vertex to is not visited, then move to it (the edge (v, to) becomes an edge of the breadth-first search tree).

if (dist[to] == -1)

{

Add vertex to to the end of the queue and compute the shortest distance dist[to].

q.push(to);

dist[to] = dist[v] + 1;

}

}

}

The main part of the program. Read the input data.

scanf("%d %d %d", &n, &s, &f);

g.resize(n + 1);

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

{

scanf("%d", &val);

if (val == 1) g[i].push_back(j);

}

Start the breadth-first search from vertex s.

bfs(s);

Print the shortest distance. If there is no path to vertex f (dist[f] < 0), set dist[f] = 0.

if (dist[f] < 0) dist[f] = 0;

printf("%d\n", dist[f]);

Algorithm realization – queue simulation

Declare an adjacency matrix g to store the graph and an array dist to store the shortest distances from the source to the vertices.

#define MAX 110

int g[MAX][MAX], dist[MAX];

The bfs function implements a breadth-first search starting from the vertex start.

void bfs(int start)

{

Initialize the dist array. If dist[i] = -1, it means that vertex i is not visited.

memset(dist,-1,sizeof(dist));

dist[start] = 0;

Initialize the queue. Implement the queue as a local array q of size MAX (at any given time, the number of vertices in the queue will not exceed the number of vertices in the graph). Head and Tail are pointers to the front and end of the queue.

int q[MAX], Head = 0, Tail = 1;

q[Head] = start;

Continue the breadth-first search as long as the queue is not empty.

while(Head < Tail)

{

Extract vertex v from the front of the queue.

int v = q[Head++];

Where can we go from vertex v? Iterate over the edges v → i.

for (int i = 1; i <= n; i++)

If there is an edge from v to i and vertex i is not visited, then move to it (the edge (v, i) becomes an edge of the breadth-first search tree).

if (g[v][i] && dist[i] == -1)

{

Add vertex i to the end of the queue and compute the shortest distance dist[i].

q[Tail++] = i;

dist[i] = dist[v] + 1;

}

}

}

The main part of the program. Read the input data.

scanf("%d %d %d",&n,&s,&f);

for(i = 1; i <= n; i++)

for(j = 1; j <= n; j++)

scanf("%d",&g[i][j]);

Start the breadth-first search from vertex s.

bfs(s);

Print the shortest distance. If there is no path to vertex f (dist[f] < 0), set dist[f] = 0.

if (dist[f] < 0) dist[f] = 0;

printf("%d\n",dist[f]);

Java realization – adjacency matrix

import java.util.*;

public class Main

{

static int g[][], dist[];

static int n, s, f;

static void bfs(int start)

{

Arrays.fill(dist,-1);

dist[start] = 0;

Queue<Integer> q = new LinkedList<Integer>();

q.add(start);

while(!q.isEmpty())

{

int v = q.poll();

for(int to = 1; to <= n; to++)

if (g[v][to] == 1 && dist[to] == -1)

{

q.add(to);

dist[to] = dist[v] + 1;

}

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

s = con.nextInt();

f = con.nextInt();

g = new int[n+1][n+1];

dist = new int[n+1];

for (int i = 1; i <= n; i++)

for (int j = 1; j <= n; j++)

g[i][j] = con.nextInt();

bfs(s);

if (dist[f] < 0) dist[f] = 0;

System.out.println(dist[f]);

con.close();

}

}

Java realization – adjacency list

import java.util.*;

public class Main

{

static ArrayList<Integer>[] g;

static int dist[];

static void bfs(int start)

{

Arrays.fill(dist,-1);

dist[start] = 0;

Queue<Integer> q = new LinkedList<Integer>();

q.add(start);

while(!q.isEmpty())

{

int v = q.poll();

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v].get(i);

if (dist[to] == -1)

{

q.add(to);

dist[to] = dist[v] + 1;

}

}

}

}

@SuppressWarnings("unchecked")

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int s = con.nextInt();

int f = con.nextInt();

g = new ArrayList[n+1];

for(int i = 0; i <= n; i++)

g[i] = new ArrayList<Integer>();

dist = new int[n+1];

for (int i = 1; i <= n; i++)

for (int j = 1; j <= n; j++)

{

int val = con.nextInt();

if (val == 1) g[i].add(j);

}

bfs(s);

if (dist[f] < 0) dist[f] = 0;

System.out.println(dist[f]);

con.close();

}

}

Python realization – adjacency matrix

Import the deque.

from collections import deque

The bfs function implements a breadth-first search starting from the vertex start.

def bfs(start):

Initialize the dist list. If dist[i] = -1, it means that vertex i is not visited.

global dist

dist = [-1] * (n + 1)

dist[start] = 0

Declare and initialize a queue q.

q = deque([start])

Continue the breadth-first search as long as the queue is not empty.

while q:

Extract and remove vertex v from the front of the queue.

v = q.popleft()

Where can we go from vertex v? Iterate over the edges v → to.

for to in range(1, n + 1):

If there is an edge from v to to and vertex to is not visited, then move to it (the edge (v, to) becomes an edge of the breadth-first search tree).

if g[v][to] == 1 and dist[to] == -1:

Add vertex to to the end of the queue and compute the shortest distance dist[to].

q.append(to)

dist[to] = dist[v] + 1

The main part of the program. Read the input data.

n, s, f = map(int, input().split())

g = [[] for _ in range(n + 1)]

for i in range(1, n + 1):

g[i] = [0] + list(map(int, input().split()))

Start the breadth-first search from vertex s.

bfs(s)

Print the shortest distance. If there is no path to vertex f (dist[f] < 0), set dist[f] = 0.

if dist[f] < 0: dist[f] = 0

print(dist[f])

Python realization – adjacency list

Import the deque.

from collections import deque

The bfs function implements a breadth-first search starting from the vertex start.

def bfs(start):

Initialize the dist list. If dist[i] = -1, it means that vertex i is not visited.

global dist

dist = [-1] * (n + 1)

dist[start] = 0

Declare and initialize a queue q.

q = deque([start])

Continue the breadth-first search as long as the queue is not empty.

while q:

Extract and remove vertex v from the front of the queue.

v = q.popleft()

Where can we go from vertex v? Iterate over the edges v → to.

for to in g[v]:

If vertex to is not visited, then move to it (the edge (v, to) becomes an edge of the breadth-first search tree).

if dist[to] == -1:

Add vertex to to the end of the queue and compute the shortest distance dist[to].

q.append(to)

dist[to] = dist[v] + 1

The main part of the program. Read the input data.

n, s, f = map(int, input().split())

Initialize and construct the adjacency list g.

g = [[] for _ in range(n + 1)]

for i in range(1, n + 1):

row = [0] + list(map(int, input().split()))

for j in range(1, n + 1):

if row[j] == 1: g[i].append(j)

Start the breadth-first search from vertex s.

bfs(s)

Print the shortest distance. If there is no path to vertex f (dist[f] < 0), set dist[f] = 0.

if dist[f] < 0: dist[f] = 0

print(dist[f])